For this year’s Google IO, we built a Crossword game and we had to experiment generating crosswords, with different layouts and sizes, to be displayed in the game.
Our goal is to create crossword puzzles from a list of words. We wanted to develop both asymmetrical and symmetrical boards to come up with an appealing layout to play with.
What sets our approach apart is its efficiency. Whether you're creating a small puzzle or one with over 80k words, our crossword generation allows for quick and efficient generation for symmetrical and asymmetrical boards.
How do we represent the crossword?
An important starting point is to know how we want to represent the puzzle in our generator. In our approach we represent the crossword as a matrix with coordinates (x, y) where each character fills a position.
Consider the following crossword:
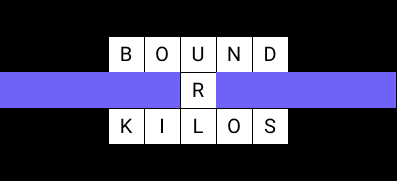
If we define the center (0, 0) where the R of the word ‘URL’ is, we would represent it as::
Overall, this approach will help us: to obtain the character at any desired location, the words that are passing through a position, ensuring words are connected, checking for overlapping words and deriving word constraints.
Understanding word connections, overlaps and constraints
The Crossword class stores the words that are placed so far, and the bounds, if any, that define the maximum board size as a rectangle. In addition, the class has methods that provide information about what adding a new word into the existing board entails, these are:
- Check that a word is connected to the board.
Adding the word "SUN" at (2, -2) would be connected:
However, adding the word "SUN" at (-2, 0) would not be connected:
- No overlapping of words. Overlapping a word means that adding such an entry would change an existing word or overwrite it completely.
Adding the word "USA" at (-5, -2) would overlap with "ALBUS":
However, adding the word "SUN" at (2, -2) would not overlap:
- Get the constraints of a position on the board.
In this next example we are going to evaluate the position (2, -2). We have three constraints, one at position 0 for the character 'S', another at position 4 for the character 'W' and invalid length of a word with 4 characters.
Constraints might also enforce invalid lengths, since otherwise a word may overlap, invalidating the crossword. Bigger and smaller words can be added, but not the exact size marked as invalid.
Sorting the words
When generating a crossword, one of the most crucial steps is finding and placing words that meet the requirements of a crossword quickly.
A slow search can significantly increase the time it takes to complete the generation. To optimize the search process, the pool of words had to be organized into a data structure that makes the lookup of fitting words faster.
Given the list of words 'Aunt', 'Addy', 'Adds' and 'Away' will structure and sort them as:
As you may notice, some words appear multiple times. Although it increases storage, this sacrifice boosts the search performance.
Now that the words are sorted, we can search for a word efficiently with the given constraints:
To showcase the increase in search performance by using this sorting system, we can see the difference in time when searching for 5 words with the different methods:
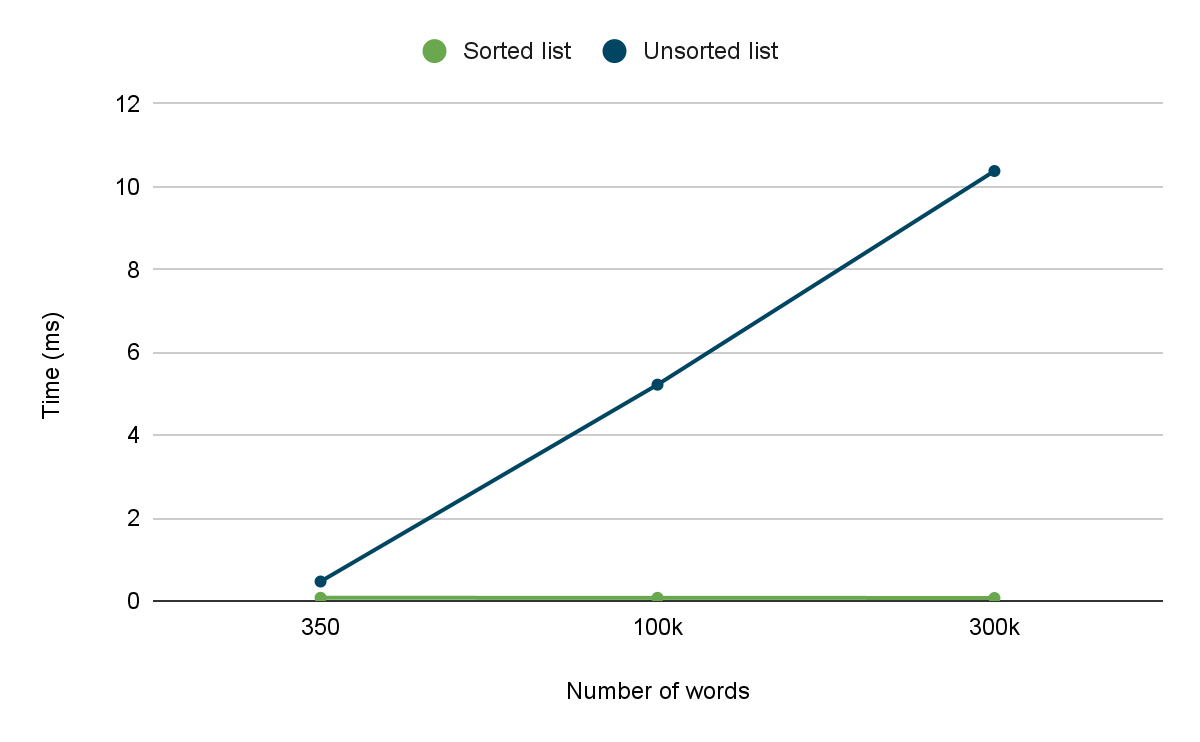
We can notice that the speed is constant in the sorted words. The bigger the list the more noticeable the performance will be, due to their asymptotic time complexities.
Generating the crossword board
Now that we have a clear understanding of how we structured the initial pool of words, how we are representing the position of the words in the board and the data model that will hold all this information, it is time to discuss how each word is placed in the crossword.
Our approach starts with a seeding phase. We select one of the largests words and place it on the board. Then we populate the board by evaluating if any of its characters allows a new word to be placed, and we continue resolving, adding and expanding the words iteratively until there are no candidates left.
How do we pick a spot to expand the board?
Expanding refers to the process of introducing a new word into the crossword. There are different algorithms we can use to determine what location should be expanded next, for example: Depth-First Search (DFS) or Breadth-First Search (BFS).
We followed the BFS approach to expand the crossword, expanding a word first entirely before continuing to the next word.
In order to optimize this process we store all the candidates that we check to place a new word. By doing this, we avoid reevaluating the same position multiple times.
Adding a word
The crossword is populated iteratively from the starting point. The process continues until there are no candidates or all the words are placed.
When searching for a word to be placed in the crossword, the strategy is to add the word with the largest length that meets the given constraints. This simple heuristic aims to increase the probabilities of finding words that can connect, since the longer the word, the more characters can be considered during expansion.
During the adding process, we perform the following steps:
- The word is added to the crossword.
- The word is removed from the pool of available words to prevent it from being used again.
- Add new candidates from the new word.
For diversified crossovers, when adding new candidate locations, we don’t just add the locations that a word spans through, but we also add those neighboring locations:
Asymmetrical Generator
In an asymmetrical crossword board, we are placing the words iteratively from the top left of the board to the bottom right. We place the initial word in the top left corner as a strategic choice because we expand from left to right and from top to bottom.
The steps to place a word from a candidate position are as follows:
- Check the constraints of the candidate.
- Search for the first word that matches the constraints.
- Place the word.
In the following image we can see that after adding the seed, we add its possible candidates, and after that we continue with the second placed word ‘identical’ iteratively until we don’t have candidates or words left.
Symmetrical Generator
In the symmetrical crossword puzzle generator, we populate the puzzle with a horizontal line of symmetry. This means that the layout of words on the top half of the board mirrors the layout on the bottom half.
The initial word needs to be placed strategically to make it grow across the area bounded by the board whilst keeping the symmetry.
The initial seed word must have an odd length, so that it crosses the line of symmetry and respects the symmetry, by aligning the middle character with the line of symmetry. In addition, the seed word is placed at the left of the bound in the x coordinate; ensuring that the crossword expands to the right.
When growing a symmetrical crossword, there are two scenarios to consider when adding a new word: it can either cross the line of symmetry, or we have to find another word with the same length to fit in its reflected position.
Crossing the Line of Symmetry
When adding a single word that crosses the line of symmetry, we have to follow the same approach as the initial seeded word. It must have an odd length to allow for the middle character of the word to align with the line of symmetry.
In practice, such scenarios are rare, depending on the word pool, finding a word with a single valid length and multiple letter constraints is unlikely to succeed.
Mirrored Placement
When we find one word on the bottom half of the board, we have to find a word of the same length on the top half of the board. If we can’t find a word with that length we will retry with a smaller length until we find a suitable match for both halves or until there are no suitable words.
This ensures that every word added has a mirrored equivalent, maintaining the symmetry.
Conclusion
Now that we have a crossword generator we can start efficiently creating boards of any size that are symmetrical or asymmetrical by specifying a list of words.
You can also create your own crossword generator with different types of symmetry extending the CrosswordGenerator class. Check out the complete open-source project and the crossword generator package!
.png)
